Logaritmo

-

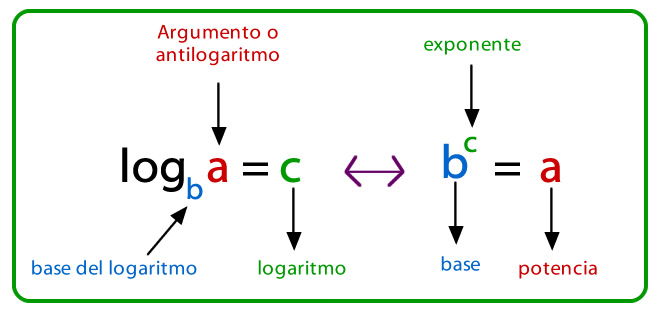
Definición de logaritmos

Seguramente has estudiado ya las potencias y sabes que, por ejemplo:

  \[10^{4}=10000\]

 Pero, supongamos que quieres encontrar una potencia a la cual elevar al número 10 y que el resultado sea 10000000. Eso se puede escribir de la siguiente forma:

\[10^{x}=10000000\]





Propiedades de los logaritmos

 

1 El logaritmo de un producto es igual a la suma de los logaritmos de los factores

 

\log(A\cdot B) = \log A + \log B

 

2 El logaritmo de un cociente es igual a la diferencia del logaritmo del dividendo y el logaritmo del divisor

 

\displaystyle\log(\frac{A}{B}) = \log A - \log B

 

3 El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base

 

\log A^{n} = n\cdot \log A

 

4El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz

 

\displaystyle \log\sqrt[n]{A} = \frac{\log A}{n} = \frac{1}{n}\cdot \log A

 

De las propiedades 3 y 4podemos deducir que:

 

\displaystyle \log\sqrt[n]{A^{m}} = \frac{m\cdot \log A}{n} = \frac{m}{n}\cdot \log A

 

5 El logaritmo base 'a' de 'a' es '1'

\log_{a}a = 1

 

6 El logaritmo de 1 es 0(Sin importar la base del logaritmo)

 

\log 1=0

 

Por lo tanto:

\log 10=1

\ln e=1

 

7 El argumento de un logaritmo siempre debe ser mayor que cero

 

Para      \log X=Y      se cumple que      X> 0

Refrencias.

M., F., Graterol, J., H., S., G., P., S., Coronel, R., S., T., S., V., S., S., B., S., G., Silva, K. P. F., . . . Calderón, R. (2019, 13 junio). Definicion y propriedades de logaritmos | Superprof. Material Didáctico - Superprof. https://www.superprof.es/apuntes/escolar/matematicas/algebra/log/logaritmos-2.html

Comentarios

Publicar un comentario